Spectral Algorithms¶
SPy implements various algorithms for dimensionality reduction and supervised & unsupervised classification. Some of these algorithms are computationally burdensome and require iterative access to image data. These algorithms will almost always execute significantly faster if the image data is loaded into memory. Therefore, if you use these algorithms and have sufficient computer memory, you should load your image into memory.
In [1]: from spectral import *
In [2]: img = open_image('92AV3C.lan').load()
Unsupervised Classification¶
Unsupervised classification algorithms divide image pixels into groups based on spectral similarity of the pixels without using any prior knowledge of the spectral classes.
k-means Clustering¶
The k-means algorithm takes an iterative approach to generating clusters.
The parameter k specifies the desired number of clusters to generate. The algorithm
begins with an initial set of cluster centers (e.g., results from cluster).
Each pixel in the image is then assigned to the nearest cluster center (using
distance in N-space as the distance metric) and each cluster center is then recomputed
as the centroid of all pixels assigned to the cluster. This process repeats until
a desired stopping criterion is reached (e.g., max number of iterations). To run
the k-means algorithm on the image and create 20 clusters, using a maximum of
50 iterations, call kmeans as follows.
In [3]: (m, c) = kmeans(img, 20, 30)
Initializing clusters along diagonal of N-dimensional bounding box.
Starting iterations.
Iteration 1...done
21024 pixels reassigned.
Iteration 2...done
11214 pixels reassigned.
Iteration 3...done
4726 pixels reassigned.
---// snip //---
Iteration 28...done
248 pixels reassigned.
Iteration 29...done
215 pixels reassigned.
Iteration 30...done
241 pixels reassigned.
^CIteration 31... 15.9%KeyboardInterrupt: Returning clusters from previous iteration
Note that I interrupted the algorithm with a keyboard interrupt (CTRL-C) after
the 30th iteration since there were only about a hundred pixels migrating between
clusters at that point. kmeans catches the KeyboardInterrupt
exception and returns the clusters generated at the end of the previous
iteration. If you are running the algorithm interactively, this feature allows
you to set the max number of iterations to an arbitrarily high number and then
stop the algorithm when the clusters have converged to an acceptable level. If you
happen to set the max number of iterations too small (many pixels are still migrating
at the end of the final iteration), you can simply call kmeans again
to resume processing by passing the cluster centers generated by the previous call
as the optional start_clusters argument to the function.

k-means clustering results¶
Notice that kmeans appears to have captured much more of the
spectral variation in the image than the single-pass cluster
function. Let’s also take a look at the the cluster centers produced by the
algorithm:
In [4]: import matplotlib.pyplot as plt
In [5]: plt.figure()
In [6]: for i in range(c.shape[0]):
...: plt.plot(c[i])
...:
In [7]: plt.grid()
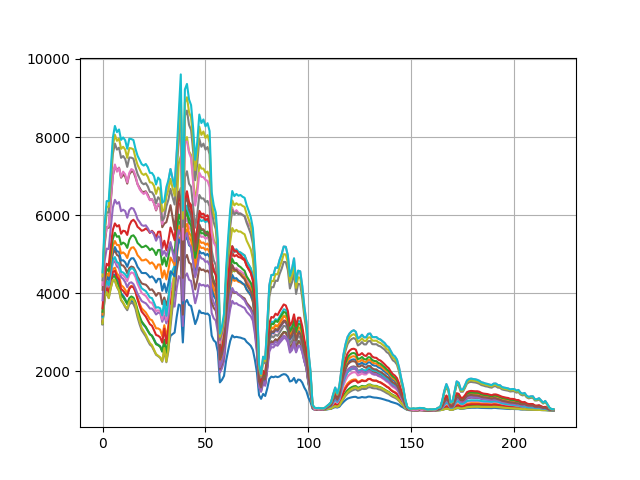
k-means cluster centers¶
Supervised Classification¶
Training Data¶
Performing supervised classification requires training a classifier with training data that associates samples with particular training classes. To assign class labels to pixels in an image having M rows and N columns, you must provide an MxN integer-valued ground truth array whose elements are indices for the corresponding training classes. A value of 0 in the ground truth array indicate an unlabeled pixel (the pixel is not associated with a training class).
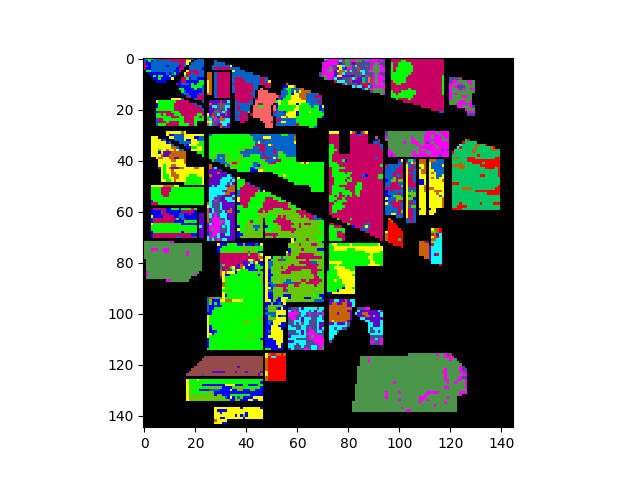
The following commands will load and display the ground truth map for our sample image:
In [8]: gt = open_image('92AV3GT.GIS').read_band(0)
In [9]: v = imshow(classes=gt)
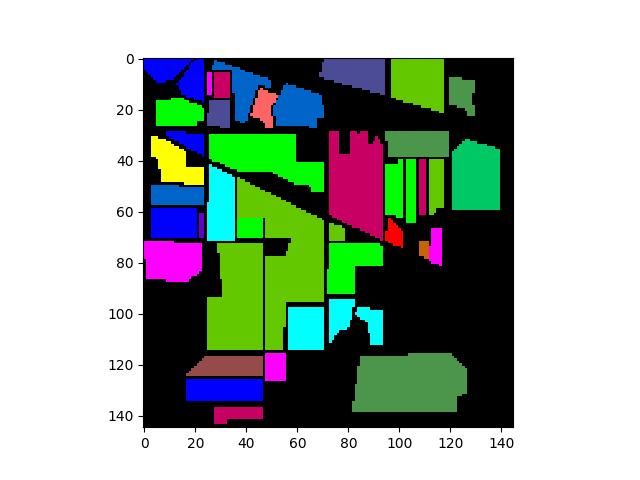
We can now create a TrainingClassSet object by calling
create_training_classes:
In [10]: classes = create_training_classes(img, gt)
With the training classes defined, we can then create a supervised classifier, train it with the training classes, and then classify an image.
Gaussian Maximum Likelihood Classification¶
In this case, we’ll perform Gaussian Maximum Likelihood Classification (GMLC), so let’s create the appropriate classifier.
In [11]: gmlc = GaussianClassifier(classes)
When we created the classifier, it was automatically trained on the training sets we provided. Notice that the classifier ignored five of the training classes. GMLC requires computing the inverse of the covariance matrix for each training class. Since our sample image contains 220 spectral bands, classes with fewer than 220 samples will have singular covariance matrices, for which we can’t compute the inverse.
Once the classifier is trained, we can use it to classify an image having the same spectral bands as the training set. Let’s classify our training image and display the resulting classification map.
In [12]: clmap = gmlc.classify_image(img)
In [13]: v = imshow(classes=clmap)
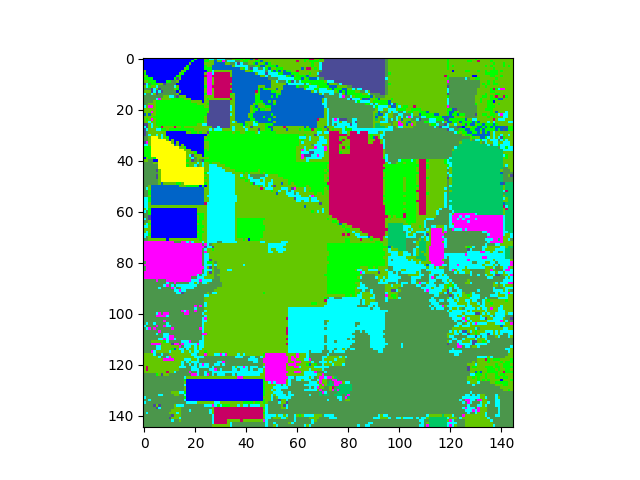
The classification map above shows classification results for the entire image. To view results for only the ground truth pixels we must mask out all the pixels not associated with a training class.
In [14]: gtresults = clmap * (gt != 0)
In [15]: v = imshow(classes=gtresults)
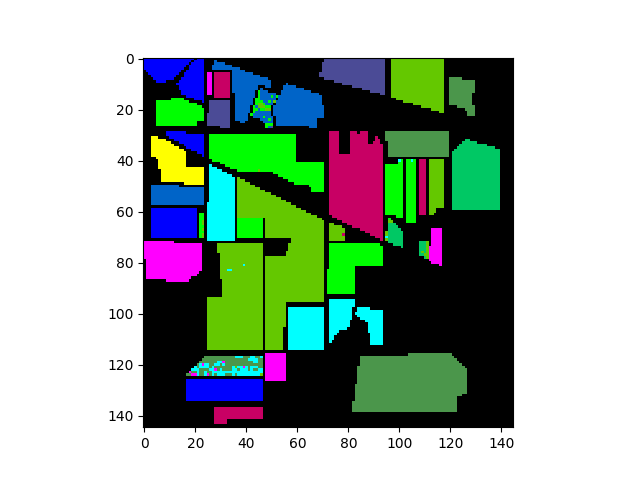
If the classification results are good, we expect the classification map
above to look very similar to the original ground truth map. To view only the
errors, we must mask out all elements in gtResults that do not match the
ground truth image.
In [16]: gterrors = gtresults * (gtresults != gt)
In [17]: v = imshow(classes=gterrors)
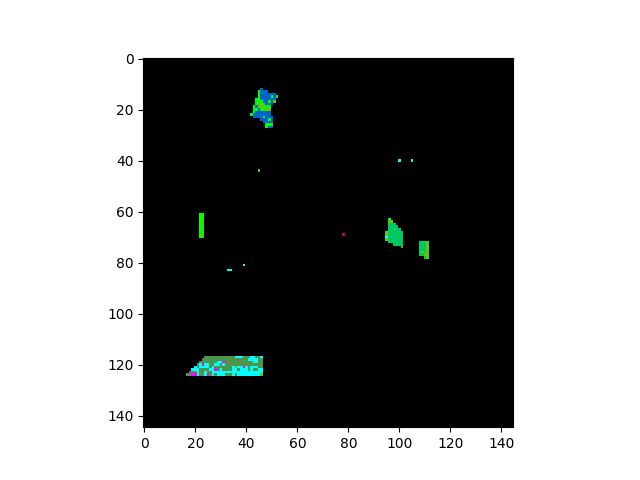
The five contiguous regions in the error image above correspond to the ground
truth classes that the GaussianClassifier ignored because they
had too few samples.
The following table lists the supervised classifiers SPy currently provides.
Classifier |
Description |
|---|---|
Gaussian Maximum Likelihood |
|
Mahalanobis Distance |
|
|
Multi-Layer Perceptron |
Dimensionality Reduction¶
Processing hyperspectral images with hundreds of bands can be computationally burdensome and classification accuracy may suffer due to the so-called “curse of dimensionality”. To mitigate these problems, it is often desirable to reduce the dimensionality of the data.
Principal Components¶
Many of the bands within hyperspectral images are often strongly correlated. The principal components transformation represents a linear transformation of the original image bands to a set of new, uncorrelated features. These new features correspond to the eigenvectors of the image covariance matrix, where the associated eigenvalue represents the variance in the direction of the eigenvector. A very large percentage of the image variance can be captured in a relatively small number of principal components (compared to the original number of bands) .
The SPy function principal_components computes the principal
components of the image data and returns the mean, covariance, eigenvalues, and
eigenvectors in a PrincipalComponents.
This object also contains a transform to rotate data in to the space of the
principal compenents, as well as a method to reduce the number of eigenvectors.
In [18]: pc = principal_components(img)
In [19]: v = imshow(pc.cov)
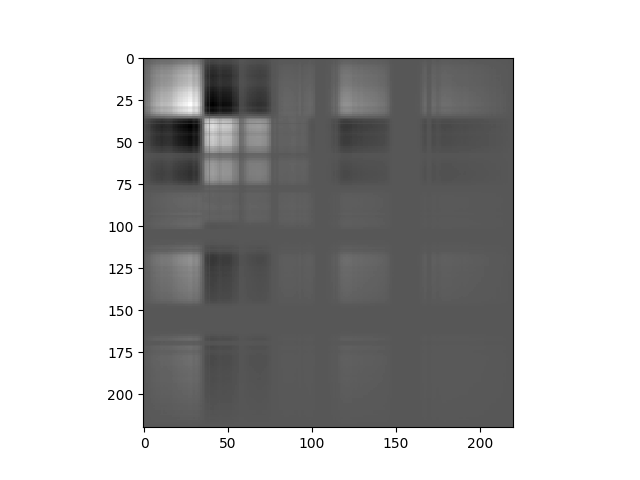
In the covariance matrix display, whiter values indicate strong positive covariance, darker values indicate strong negative covariance, and grey values indicate covariance near zero.
To reduce dimensionality using principal components, we can sort the eigenvalues in descending order and then retain enough eigenvalues (an corresponding eigenvectors) to capture a desired fraction of the total image variance. We then reduce the dimensionality of the image pixels by projecting them onto the remaining eigenvectors. We will choose to retain a minimum of 99.9% of the total image variance.
In [20]: pc_0999 = pc.reduce(fraction=0.999)
In [21]: # How many eigenvalues are left?
In [22]: len(pc_0999.eigenvalues)
Out[22]: 32
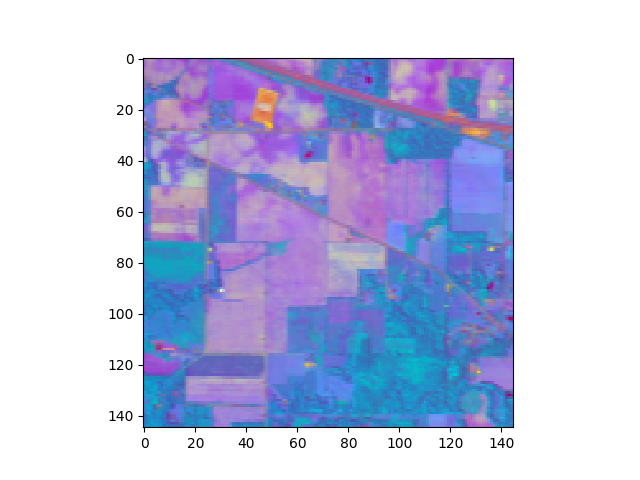
In [23]: img_pc = pc_0999.transform(img)
In [24]: v = imshow(img_pc[:,:,:3], stretch_all=True)
Now we’ll use a Gaussian maximum likelihood classifier (GMLC) for the reduced principal components to train and classify against the training data.
In [25]: classes = create_training_classes(img_pc, gt)
In [26]: gmlc = GaussianClassifier(classes)
In [27]: clmap = gmlc.classify_image(img_pc)
In [28]: clmap_training = clmap * (gt != 0)
In [29]: v = imshow(classes=clmap_training)
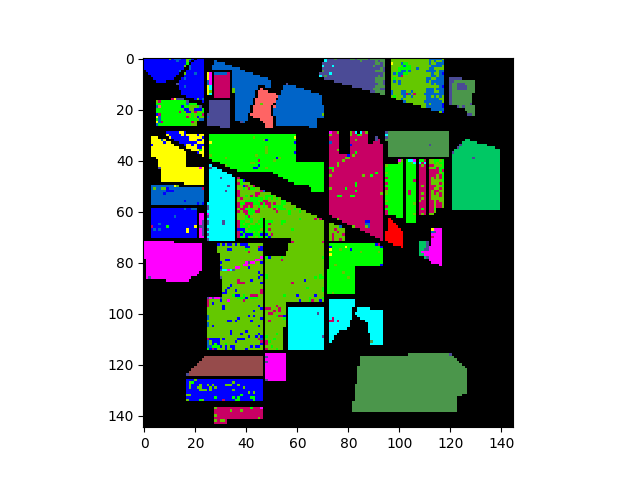
And the associated errors:
In [30]: training_errors = clmap_training * (clmap_training != gt)
In [31]: v = imshow(classes=training_errors)
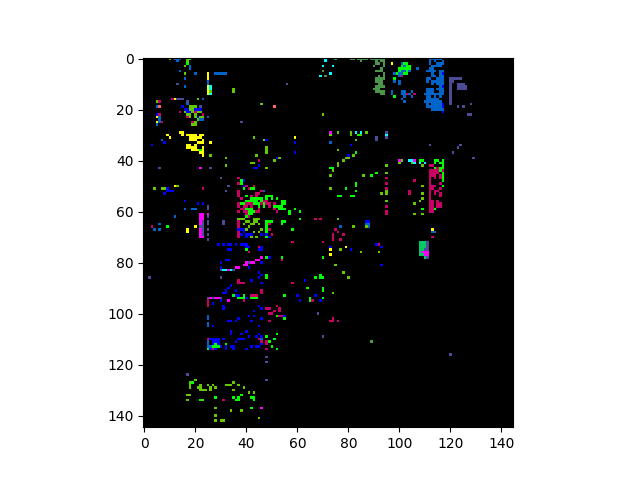
Fisher Linear Discriminant¶
The Fisher Linear Discriminant (a.k.a., canonical discriminant) attempts to find a set of transformed axes that maximize the ratio of the average distance between classes to the average distance between samples within each class. [Richards1999] This is written as
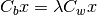
where 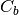 is the covariance of the class centers and
is the covariance of the class centers and 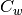 is the
weighted average of the covariances of each class. If
is the
weighted average of the covariances of each class. If 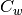 is invertible,
this becomes
is invertible,
this becomes
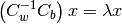
This eigenvalue problem is solved by the linear_discriminant
function, yielding C-1 eigenvalues, where C is the number of classes.
In [32]: classes = create_training_classes(img, gt)
In [33]: fld = linear_discriminant(classes)
In [34]: len(fld.eigenvectors)
Out[34]: 220
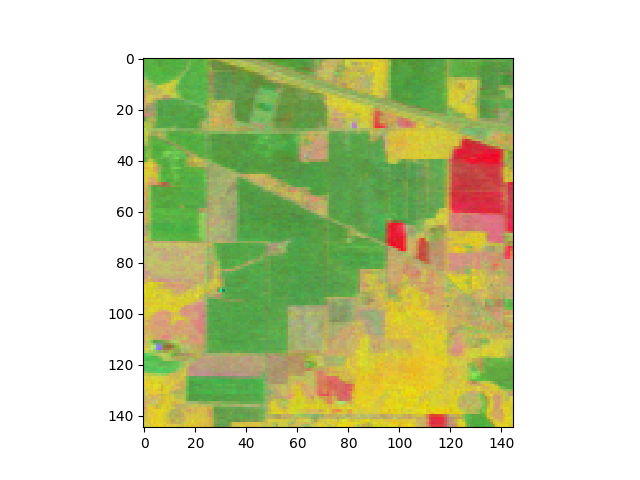
Let’s view the image projected onto the top 3 components of the transform:
In [35]: img_fld = fld.transform(img)
In [36]: v = imshow(img_fld[:, :, :3])
Next, we’ll classify the data using this discriminant.
In [37]: classes.transform(fld.transform)
In [38]: gmlc = GaussianClassifier(classes)
In [39]: clmap = gmlc.classify_image(img_fld)
In [40]: clmap_training = clmap * (gt != 0)
In [41]: v = imshow(classes=clmap_training)
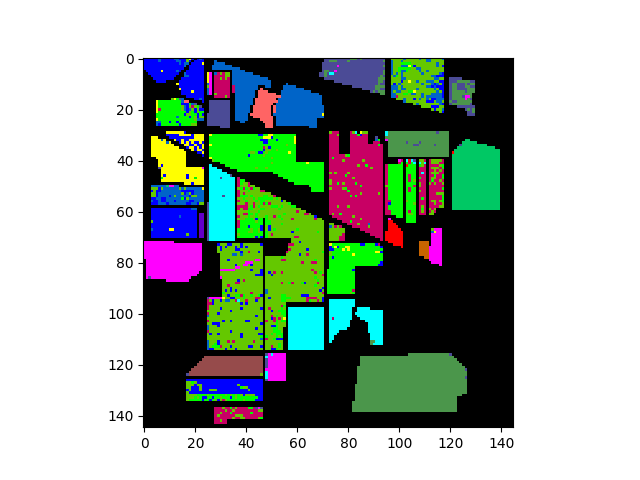
In [42]: fld_errors = clmap_training * (clmap_training != gt)
In [43]: v = imshow(classes=fld_errors)
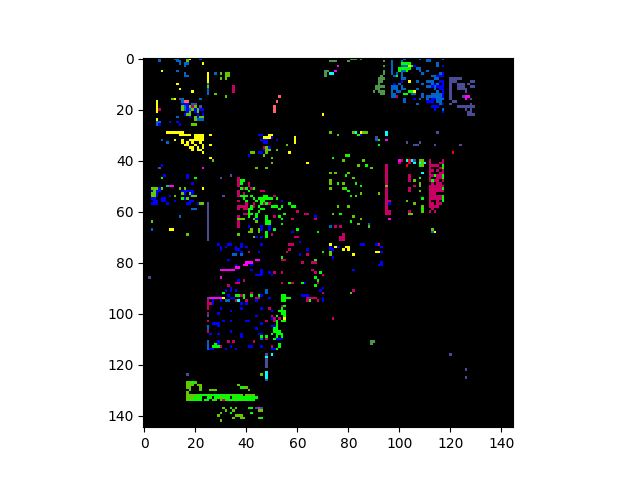
Target Detectors¶
RX Anomaly Detector¶
The RX anomaly detector uses the squared Mahalanobis distance as a measure of
how anomalous a pixel is with respect to an assumed background. The SPy
rx function computes RX scores for an
array of image pixels. The squared Mahalanobis distance is given by
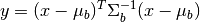
where 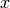 is the pixel spectrum,
is the pixel spectrum, 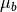 is the background
mean, and
is the background
mean, and 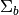 is the background covariance [Reed_Yu_1990].
is the background covariance [Reed_Yu_1990].
If no background statistics are passed to the rx function,
background statistics will be estimated from the array of pixels for which the
RX scores are to be calculated.
In [44]: rxvals = rx(img)
To declare pixels as anomalous, we need to specify a threshold RX score. For example, we could choose all image pixels whose RX score has a probability of less than 0.001 with respect to the background:
In [45]: from scipy.stats import chi2
In [46]: nbands = img.shape[-1]
In [47]: P = chi2.ppf(0.999, nbands)
In [48]: v = imshow(1 * (rxvals > P))
Rather than specifying a threshold for anomalous pixels, one can also simply view an image of raw RX scores, where brighter pixels are considered “more anomalous”:
In [49]: v = imshow(rxvals)

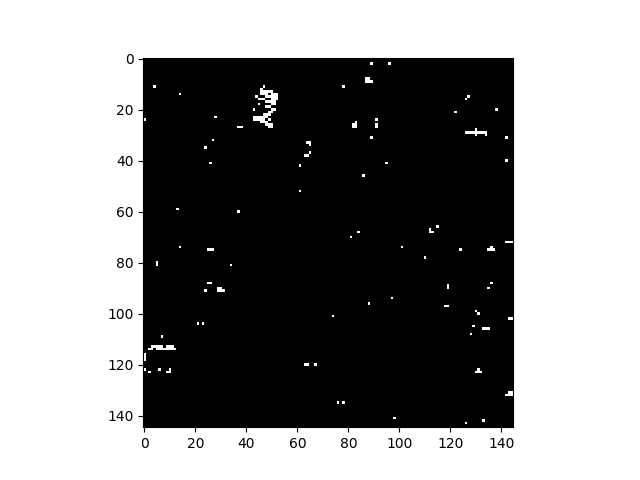
For the sample image, only a few pixels are visible in the image of RX scores because a linear color scale is used and there is a very small number of pixels with RX scores much higher than other pixels. This is apparent from viewing the histogram of the RX scores.
In [50]: import matplotlib.pyplot as plt
In [51]: f = plt.figure()
In [52]: h = plt.hist(rxvals.ravel(), 200, log=True)
In [53]: h = plt.grid()
The outliers are not obvious in the histogram, so let’s print their values:
In [54]: print(np.sort(rxvals.ravel())[-10:])
[ 665.17211462 675.85801536 683.58190673 731.4872873 739.95211335
906.98669373 956.49972325 1703.20957949 2336.11246149 9018.65517253]
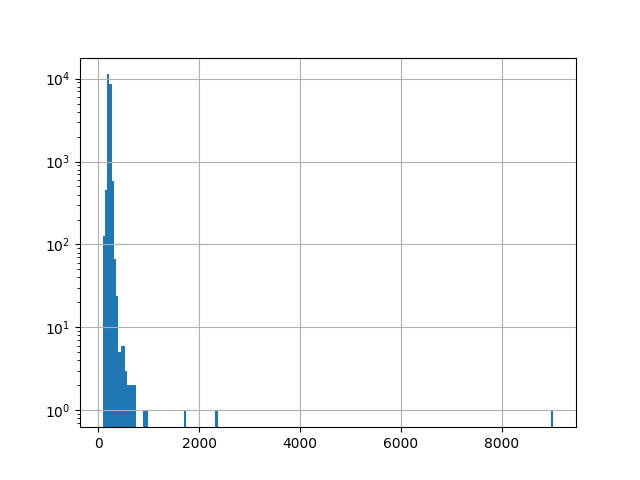
To view greater detail in the RX image, we can adjust the lower and upper limits of the image display. Since we are primarily interested in the most anomalous pixels, we will set the black level to the 99th percentile of the RX values’ cumulative histogram and set the white point to the 99.99th percentile:
In [55]: v = imshow(rxvals, stretch=(0.99, 0.9999))
We can see the new RGB data limits by inspecting the returned
ImageView object:
In [56]: print(v)
ImageView object:
Display bands : [0]
Interpolation : <default>
RGB data limits :
R: [291.6938067178437, 956.4997232540622]
G: [291.6938067178437, 956.4997232540622]
B: [291.6938067178437, 956.4997232540622]
Note that we could also have set the contrast stretch to explicit RX values (vice percentile values) by specifying the bounds keyword instead of stretch.
If an image contains regions with different background materials, then the assumption of a single mean/covariance for background pixels can reduce performance of the RX anomaly detector. In such situations, better results can be obtained by dynamically computing background statistics in a neighborhood around each pixel being evaluated.
To compute local background statistics for
each pixel, the rx function accepts an optional window argument, which
specifies an inner/outer window within which to calculate background statistics
for each pixel being evaluated. The outer window is the window within which
background statistics will be calculated. The inner window is a smaller window
(within the outer window) indicating an exclusion zone within which pixels are
to be ignored. The purpose of the inner window is to prevent potential anomaly/target
pixels from “polluting” background statistics.
For example, to compute RX scores with background statistics computed from a
21 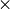 21 pixel window about the pixel being evaluated, with an exclusion window of
5
21 pixel window about the pixel being evaluated, with an exclusion window of
5 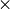 5 pixels, the function would be called as follows:
5 pixels, the function would be called as follows:
In [57]: rxvals = rx(img, window=(5,21))
While the use of a windowed background will often improve results for images containing
multiple background materials, it does so at the expense of introducing two
issues. First, the sizes of the inner and outer windows must be specified such
that the resulting covariance has full rank. That is, if 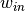 and
and
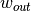 represent the pixel widths of the inner and outer windows, respectively,
then
represent the pixel widths of the inner and outer windows, respectively,
then 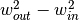 must be at least as large as the number of
image bands. Second, recomputing the estimated background covariance for each
pixel in the image makes the computational complexity of of the RX score
computation orders of magnitue greater.
must be at least as large as the number of
image bands. Second, recomputing the estimated background covariance for each
pixel in the image makes the computational complexity of of the RX score
computation orders of magnitue greater.
As a compromise between a fixed background and recomputation of mean & covariance
for each pixel, rx can be passed a global covariance estimate in addition
to the window argument. In this case, only the background mean within the window will
be recomputed for each pixel. This significanly reduces computation time
for the windowed algorithm and removes the size limitation on the window (except
that the outer window must be larger than the inner). For example, since our sample image has ground
cover classes labeled, we can compute the average covariance over those ground
cover classes and use the result as an estimate of the global covariance.
In [58]: C = cov_avg(img, gt)
In [59]: rxvals = rx(img, window=(5,21), cov=C)
Matched Filter¶
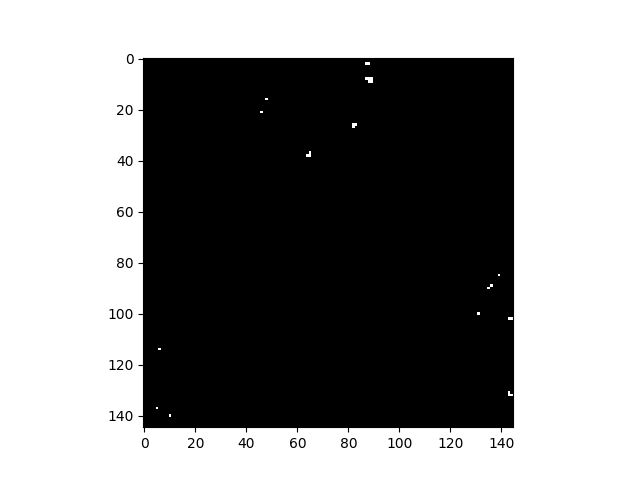
The matched filter is a linear detector given by the formula
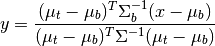
where 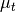 is the target mean,
is the target mean, 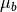 is the background
mean, and
is the background
mean, and 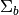 is the covariance. The matched filter response is
scaled such that the response is zero when the input is equal to the background
mean and equal to one when the pixel is equal to the target mean. Like the
is the covariance. The matched filter response is
scaled such that the response is zero when the input is equal to the background
mean and equal to one when the pixel is equal to the target mean. Like the
rx function the SPy
matched_filter function will estimate
background statistics from the input image if no background statistics are
specified.
Let’s select the image pixel at (row, col) = (8, 88) as our target, use a global background statistics estimate, and plot all pixels whose matched filter scores are greater than 0.2.
In [60]: t = img[8, 88]
In [61]: mfscores = matched_filter(img, t)
In [62]: v = imshow(1 * (mfscores > 0.2))
As with the rx function, matched_filter can be applied using
windowed background statistics (optionally with a global covariance estimate).
Miscellaneous Functions¶
Band Resampling¶
Comparing spectra measured with a particular sensor to spectra collected by a different sensor often requires resampling spectra to a common band discretization. Spectral bands of a single sensor may drift enough over time such that spectra collected by the same sensor at different dates requires resampling.
For resampling purposes, SPy treats a sensor as having Gaussian spectral response
functions for each of its spectral bands. A source sensor band will contribute
to any destination band where there is overlap between the FWHM of the response
functions of the two bands. If there is an overlap, an integral is
performed over the region of overlap assuming the source band data value is
constant over its FWHM (since we do not know the true spectral load over the
source band) and the destination band has a Gaussian response function. Any
target bands that do not have an overlapping source band will produce NaN
as the resampled band value. If FWHM information is not available for a sensor’s
bands, each band’s FWHM is assumed to reach half the distance the its adjacent
bands. Resampling results are better when source bands are at a higher spectral
resolution than the destination bands.
To create BandResampler object, we can either pass it a
BandResampler object for each sensor or
a list of band centers and, optionally, a list of FWHM values. Once the
BandResampler is created, we can call it with a source sensor spectrum and it will
return the resampled spectrum.
In [63]: import spectral.io.aviris as aviris
In [64]: img1 = aviris.open('f970619t01p02_r02_sc04.a.rfl', 'f970619t01p02_r02.a.spc')
In [65]: bands2 = aviris.read_aviris_bands('92AV3C.spc')
In [66]: resample = BandResampler(img1.bands, bands2)
In [67]: x1 = img1[96, 304]
In [68]: x2 = resample(x1)
NDVI¶
The Normalized Difference Vegetation Index (NDVI) is an indicator of the presence of vegetation. The index is commonly defined as
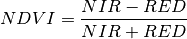
where NIR is the reflectance in the near infrared (NIR) part of the spectrum and RED is the reflectance of the red band. For our sample image, if we take band 21 (607.0 nm) for our red band and band 43 (802.5 nm) for near infrared, we get the following NDVI image.
In [69]: vi = ndvi(img, 21, 43)
In [70]: v = imshow(vi)
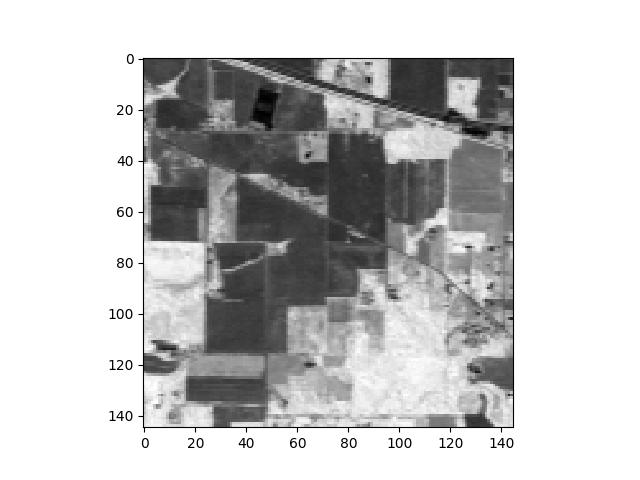
ndvi is a simple convenience function.
You could just as easily calculate the vegetation index yourself like this:
In [71]: red = img.read_band(21)
In [72]: nir = img.read_band(43)
In [73]: vi = (nir - red) / (nir + red)
Spectral Angles¶
A spectral angle refers to the angle between to spectra in N-space. In the absence of covariance data, spectral angles can be used for classifying data against a set of reference spectra by selecting the reference spectrum with which the unknown spectrum has the smallest angle.
To classify our sample image to the ground truth classes using spectral angles,
we must compute the spectral angles for each pixel with each training class mean.
This is done by the spectral_angles function.
Before calling the function, we must first create a CxB array of training class
mean spectra, where C is the number of training classes and B is the number
of spectral bands.
In [74]: import numpy as np
In [75]: classes = create_training_classes(img, gt, True)
In [76]: means = np.zeros((len(classes), img.shape[2]), float)
In [77]: for (i, c) in enumerate(classes):
....: means[i] = c.stats.mean
....:
In the code above, the True parameter to
create_training_classes forces calculation
of statistics for each class. Next, we call spectral_angles,
which returns an MxNxC array, where M and N are the number of rows and
columns in the image and there are C spectral angle for each pixel. To select
the class with the smallest angle, we call the numpy argmin
function to select the index for the smallest angle corresponding to each pixel.
The clmap + 1 is used in the display command because our class IDs start at 1 (not 0).
In [78]: angles = spectral_angles(img, means)
In [79]: clmap = np.argmin(angles, 2)
In [80]: v = imshow(classes=((clmap + 1) * (gt != 0)))
See also
msam: Modified Spectral Angle Mapper
References
- Richards1999
Richards, J.A. & Jia, X. Remote Sensing Digital Image Analysis: An Introduction. (Springer: Berlin, 1999).
- Reed_Yu_1990
Reed, I.S. and Yu, X., “Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution,” IEEE Trans. Acoust., Speech, Signal Processing, vol. 38, pp. 1760-1770, Oct. 1990.